C语言中的浮点数分为单精度和双精度，单精度的float采用32位二进制（4字节）来存储，而双精度的double使用64位（8字节）来存储。在计算机内存的存储方式都是遵从IEEE的规范的，float遵从的是IEEE R32.24，double遵从的是R64.53。
一、浮点数存储方式的分类
在计算机的发展过程中，出现了两类存储方式，分别是定点实数存储和浮点实数存储方式：
1.定点实数存储方式：约定整数位和小数位的存储长度，比如高两位放整数位，低两位放小数位。
优点是方便计算；缺点是存储的数据范围有限。
2.浮点数存储方式：用一部分二进制位存放小数点位置，称为指数域，其他全部用来存储没有小数点时的数据和符号，称为数据为和符号位。
优点是存储的数据范围更大；缺点是计算比定点实数存储慢些。
二、浮点实数存储方式
无论是单精度还是双精度，在内存的存储中都分为3个部分：
1.符号位（Sign）：0代表正数，1代表负数。
2.指数位（Exponent）：用于存储科学计数法中的指数数据，并且采用移位存储。
3.尾数部分（Mantissa）：尾数
由于指数为负，所以规定了指数位的值=科学计数法中的指数+127。
则float的存储方式如下图所示：
double的存储方式如下图：
如何把浮点数转为二进制数？
以12.15为例，整数部分我们都是十进制转二进制的方法
从最低开始往左代表，为20、21、22、23、24…所以小数的表示从20往右，分别代表2-1、2-2、2-3、2-4…
0.25 = 2-2,所以12.25转换成二进制即1100.01，即：
用科学计数法表示为1.10001*103，存储时，符号位为0，指数位为3+127 = 130 ，转换成二进制为：
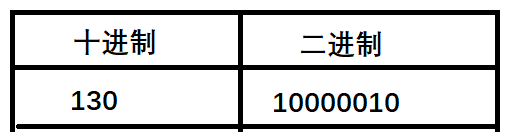
尾数位为100011，所以在小端模式下存储为：
为什么浮点数存在精度问题
以1.3这个有穷数为例，0.3 = 2-2+2-5+2-6+2-9+2-10+2-13……
转换成二进制变成了1.0100110011001100110011001…变成了无穷数。这个时候只能在第23位舍0进1，即：
1.0100110011001100110010
由于在转换过程中，丢失了位数，所以这只是近似值，如果把这个近似数转换为十进制小数，会得到1.1258290，这就是为什么在比较浮点数相等时，一般建议使用区间值而不是直接等值比较，而由于这种编码方式，可以发现，绝对值越大的数，精度越大，因为绝对值越大时，整数部分占太多位置，小数部分舍弃的多。
double类型如何存储
double类型是双精度类型，在32位操作系统中占8字节，double类型的编码方式跟float类型是差不多的，也是分为符号位、指数位、尾数位，只是长度跟float不同。其中符号位占一位、指数位占11位，指数位的值=指数+1023，剩下的位数存尾数。
3279916262